1. NALOGA:
Izdelati je potrebno program, ki bo prikazal zicni model kvadrikov in superkvadrikov z moznostjo izbire osnovnih parametrov oblike.
2. ABSTRACT:
Superquadrics are three-dimensional extensions of Piet Heins two-dimensional superelipses. They allow us to easly represent rounded, square, cylinrical, pinched and toroidal shapes with relatively simple equations. The superquadric parametric surface function is a profile surface based on trigonometric functions raised to exponents.
There are six shape parameters of superquadrics:
Program is generated in C and representation of model is made by graphical libraries of OpenGl. Data for parameters (n, e, Ax, Ay, Az and ALFA) enter into program from file param.txt, which is manualy generated. Parameters must be writen in column. To draw other model, change data in file param.txt and restart program.
Program allows rotating around x-axis by arrows UP-DOWN, around z-axis by arrows LEFT-RIGHT, approaching to the model by a or A and deviating by q or Q.
3. SUPERKVADRIKI:
Superkvadriki so razširitev osnovnih enacb kvadrikov definiranih kot sfericni produkt v parametricnem 3D prostoru. Implicitna enacba Piet-Heinove superelipse je
![]() ,kjer je e konstanta.
,kjer je e konstanta.
To enacbo lahko zapišemo v parametricni obliki
![]() -p Ł q Ł p
-p Ł q Ł p
kjer je e vzhodno/zahodni parameter ali parameter zaokrozitve robu.
Z razširitevijo superelips v prostor dobimo enacbe za elipsoide in toroide. Implicitna enacba toroida (elipsoida) je:
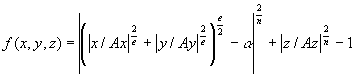
za toroid je a >1, za elipsoid pa je a = 0.
Superkvadriki omogocajo predstavitev okroglih, kvadratnih, stozcastih, toroidnih in valjcnih oblik z relativno enostavnimi enacbami. Funkcija oblike površine temelji na potenciranih trigonometricnih enacbah.
3.1 Enacba superkvadrika
Za elipsoide je parametricna enacba definirana:
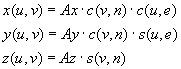
|
-p /2 Ł v Ł p /2 |
-p Ł u Ł p |
in podobno za toroide:
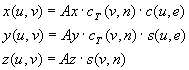
|
-p /2 Ł v Ł p /2 |
-p Ł u Ł p |
Podfunkcije uporabljene v zgornjih enacbah so definirane:
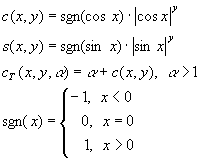
3.2 Oblika superkvadrika
Obliko superkvadrika dolocajo:
Obliko superkvadrika spreminjamo s šestimi parametri:
S sprememinjanjem parametra n se menja oblika oboda sever-jug, s parametrom e pa oblika oboda vzhod-zahod:
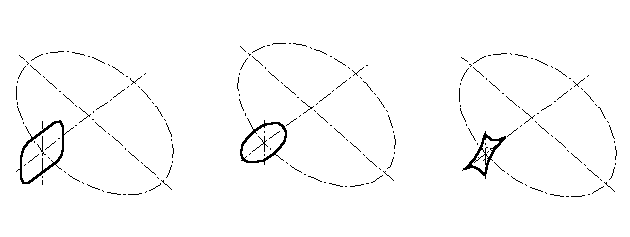
|
n ® 0 |
n =1 |
n > 1 |
Slika 1:Parameter oboda S-J
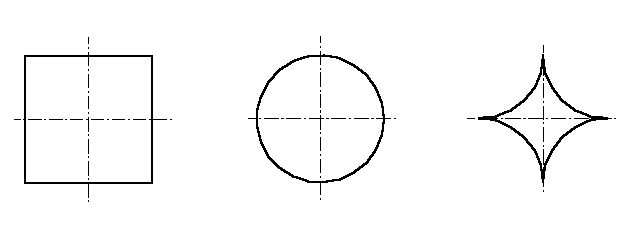
|
e ® 0 |
e =1 |
e > 1 |
Slika 2:Parameter oboda V-Z
Parametri Ax, Ay, Az in a so parametri dimenzij:
4. DATOTEKA param.txt IN KODA SuperQuadrics:
4.1 Primer vhodne datoteke "primer.txt"
3.5 - parameter ALFA
2.0 - parameter Ax
1.0 - parameter Ay
1.0 - parameter Az
2.3 - parameter n
0.8 - parameter e
4.2 Koda SuperQuadrics
#include "glos.h"
#include <GL/gl.h>
#include <GL/glu.h>
#include <GL/glaux.h>
#include <math.h>
#include <iostream.h>
#include <stdio.h>
sign(float x);
float c(float x,float y);
float s(float x,float y);
float cT(float x,float y,float z);
float x(float x,float y,float z);
float y(float x,float y,float z);
float z(float x);
void Model(void);
void CALLBACK Prikaz(void);
void CALLBACK Okno(GLsizei w, GLsizei h);
#define PI 3.141592654
float ALFA,Ax,Ay,Az,e,n;
float u,v;
struct Koord
{
float X,Y,Z;
};
Koord T[19][19];
int Kot_x ,Kot_y ,Kot_z;
float p=1;
// ROTIRANJE S KURZORSKIMI TIPKAMI IN SCALIRANJE
void CALLBACK Rotacija_Gor (void)
{
Kot_x = (Kot_x - 15) % 360;
}
void CALLBACK Rotacija_Dol (void)
{
Kot_x = (Kot_x + 15) % 360;
}
void CALLBACK Rotacija_Levo (void)
{
Kot_z = (Kot_z - 15) % 360;
}
void CALLBACK Rotacija_Desno (void)
{
Kot_z = (Kot_z + 15) % 360;
}
void CALLBACK Oddaljuje_Pogled (void)
{
p = p - 0.1;
}
void CALLBACK Priblizuje_Pogled (void)
{
p = p + 0.1;
}
void CALLBACK Hiter_Prikaz(void)
{
Prikaz(); //ponoven izris modela
}
// IZRACUN POSAMEZNE KOORDINATE
//tocka x
float x(float x,float y,float z)
{
float w;
w=Ax*cT(y,n,z)*c(x,e);
return(w);
}
//tocka y
float y(float x,float y,float z)
{
float w;
w=Ay*cT(y,n,z)*s(x,e);
return(w);
}
//tocka z
float z(float x)
{
float y;
y=Az*s(x,n);
return(y);
}
//funkcija cT
float cT(float x,float y,float z)
{
float w;
w=c(x,y)+z;
return (w);
}
//funkcija s
float s(float x, float y)
{
float z;
if (fabs(sin(x))<0.0001 && y<=0)
z=0.0;
else
z=sign(sin(x))*pow(fabs(sin(x)),y);
return (z);
}
//funkcija c
float c(float x, float y)
{
float z;
if (fabs(cos(x))<0.0001 && y<=0)
z=0.0;
else
z=sign(cos(x))*pow(fabs(cos(x)),y);
return (z);
}
//signum funkcija
sign(float x)
{
int y;
if (x<0)
y=-1.;
else if (x>0)
y=1.;
else
y=0.;
return(y);
}
// BRANJE DATOTEKE S PARAMETRI: ALFA, Ax, Ay, Az, n in e
void Branje(void)
{
FILE *param;
param=fopen("param.txt","r");
fscanf(param,"%f\n",&ALFA);
fscanf(param,"%f\n",&Ax);
fscanf(param,"%f\n",&Ay);
fscanf(param,"%f\n",&Az);
fscanf(param,"%f\n",&n);
fscanf(param,"%f\n",&e);
fclose(param);
}
// IZRIS MODELA
void Model(void)
{
//izracun tock
int i,j;
for(i=0, u=-PI;u<=PI;i++, u=u+PI/9.)
{
for (j=0, v=-PI;v<=PI;j++, v=v+PI/9.)
{
T[i][j].X=x(u,v,ALFA);
T[i][j].Y=y(u,v,ALFA);
T[i][j].Z=z(v);
}
}
glNewList(1, GL_COMPILE);
//izris v vodoravnih crt
for (i=0;i<18;i++)
{
for (int j=0;j<19;j++)
{
glBegin(GL_LINES);
glColor3f (1.0, 0.0, 0.0);
glVertex3f(T[i][j].X, T[i][j].Y, T[i][j].Z);
glVertex3f(T[i+1][j].X, T[i+1][j].Y, T[i+1][j].Z);
glEnd();
}
}
//izris v navpicnih crt
for (i=0;i<19;i++)
{
for (j=0;j<18;j++)
{
glBegin(GL_LINES);
glColor3f (1.0, 0.0, 0.0);
glVertex3f(T[i][j].X, T[i][j].Y, T[i][j].Z);
glVertex3f(T[i][j+1].X, T[i][j+1].Y, T[i][j+1].Z);
glEnd();
}
}
glEndList();
}
// ROTACIJA MODELA IN SCALIRANJE
void CALLBACK Prikaz(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f (1.0, 0.0, 0.0);
glPushMatrix();
glRotatef (Kot_x, 1, 0, 0);
glRotatef (Kot_y, 0, 1, 0);
glRotatef (Kot_z, 0, 0, 1);
glScalef (p,p,p);
glCallList(1);
glPopMatrix();
glFlush();
auxSwapBuffers();
}
// SPREMINJANJE OKNA
void CALLBACK Okno(GLsizei w, GLsizei h)
{
if (!h) return;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, 1, 1.0, 50.0); //globina izrisa
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef (0.0, 0.0, -20); //visina gledanja
}
int main(void)
{
auxInitDisplayMode (AUX_DOUBLE | AUX_RGB | AUX_DEPTH16);
auxInitPosition (0, 0, 500, 500);
auxInitWindow ("SuperQuadric");
Branje();
Model();
//skaliranje
auxKeyFunc (AUX_q, Oddaljuje_Pogled);
auxKeyFunc (AUX_a, Priblizuje_Pogled);
auxKeyFunc (AUX_Q, Oddaljuje_Pogled);
auxKeyFunc (AUX_A, Priblizuje_Pogled);
//tipke za rotiranje
auxKeyFunc (AUX_UP, Rotacija_Gor);
auxKeyFunc (AUX_DOWN, Rotacija_Dol);
auxKeyFunc (AUX_LEFT, Rotacija_Levo);
auxKeyFunc (AUX_RIGHT, Rotacija_Desno);
//funkcije za obnavljanje
auxReshapeFunc (Okno);
auxIdleFunc (Hiter_Prikaz);
auxMainLoop(Prikaz);
return(0);
}
5. RAZLAGA KODE:
Model je razdeljen na 18 delov v vodoravni in navpicni smeri. Tocke na površini modela se izracunavajo v naslednjih dveh zankah:
for(i=0, u=-PI;u<=PI;i++, u=u+PI/9.)
{
for (j=0, v=-PI;v<=PI;j++, v=v+PI/9.)
{
T[i][j].X=x(u,v,ALFA);
T[i][j].Y=y(u,v,ALFA);
T[i][j].Z=z(v);
}
}
Izracunane tocke se vpisujejo v polje T[19][19]. Širina polja je 19, ker je 19 izracunanih tock, vendar sta prva T[i][0] in zadnja T[i][18] tocka enaki.
Izris modela poteka tako, da posamezne tocke med sabo povezemo z ravno crto (atribut GL_LINES). Spodnja procedura izriše crte (povezave med tockami) samo v eni smeri (vodoravno). Pri istem indeksu j se povezeta tocki z indeksom i in i+1. Za navpicne crte pa ostaja isti indeks i in se povezeta tocki j in j+1. Procedura glVertex3f (x,y,z) izriše tocko float x,y,z. Procedura glColor3f (x,y,z) doloci barvo. Števila x,y,z so realna in x je za rdeco, y za zeleno in z za modro barvo.
for (i=0;i<18;i++)
{
for (int j=0;j<19;j++)
{
glBegin(GL_LINES);
glColor3f (1.0, 0.0, 0.0);
glVertex3f(T[i][j].X, T[i][j].Y, T[i][j].Z);
glVertex3f(T[i+1][j].X, T[i+1][j].Y, T[i+1][j].Z);
glEnd();
}
}
Zaradi hitrejšega racunaja je izris postavljen v listo glNewList. Procedure znotraj liste se izvajajo hitreje. Lista se zakljuci z glEndList.
6. ZAKLJUCEK:
Za izracun tock sem uporabil enacbe za toroid:
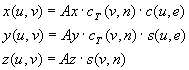
|
-p Ł v Ł p |
-p Ł u Ł p |
Z nastavitvijo parametra a enacbe toroida postanejo enacbe elipsoida. Pri elipsoidih so tocke dvakrat preracunane in izrisane zaradi parametra v, ki obtece cel krog (-p Ł v Ł p ). Potrebno pa bi bilo samo od -p /2 do p /2.
Koda programa je generirana v C-jeziku, izris modela pa je narejen z graficnimi knjiznjicami OpenGL. Vnos parametrov v program je iz datoteke param.txt, ki jo rocno generiramo. Parametri morajo biti napisani v stolpcu. Ce zelimo izris modela z drugacnimi parametri, jih moramo zamenjati v datoteki param.txt in ponovno pognati program.
Program izriše model z crtami in omogoca vrtenje izrisanega modela okrog x-osi s kurzoskima tipkama gor-dol in okrog z-osi s kurzorskima tipkama levo-desno ter priblizevanje s tipko a oz. A in oddaljevanje modela s tipko q oz.Q.
Ales Oblak
Ljubljana, 6.7. 1998