Bostjan Gustin
4.1.2000
A lot of time passed from when the man first encountred the reflection of his figure on a water surface. But it was not until the apparition of the first reflective telescopes in 1663 that mathematical calculation of reflected light rays went into consideration.
The program ACOTRACE will show us a simple way to simulate the path of a light beam, reflected by spheres, placed into space, with some hints on how could such a program be used to evaluate telescope optics.
-------------------------------------
2.2.Dolocitev mesta zadetka krogle z zarkom
2.3.Dolocitev smeri zarka po odboju
Na področju optčnih naprav se odboj svetlobe zadnje čase vse več uporablja. čeprav so bili prvi daljnogledi zgrajeni iz leč in so izkoriščali zakon LOMA svetlobe, se danes v profesionalnih astronomskih observatorijih uporablja izključno zrcalne daljnoglede.
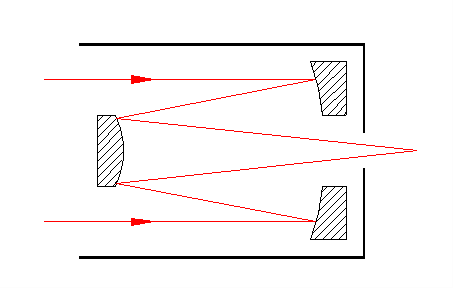
Ena najpomembnejših karakteristik vsake optike je ostrina. Najboljši način za oceniti ostrino slike je ravno kontrola poti konusa konvergirajočih žarkov svetlobe skozi napravo, ki naj bi se v idealnem primeru na goriščni ravnini združili v eno točko (Slika A):

SlikaA: Pot svetlobnih žarkov skozi optično napravo.
Ker v realnosti temu ni tako, dobimo namesto ostre točke nek zmazek: večji je zmazek, manj ostra je slika.
čeprav naš program ni direktno vezan na daljnoglede, so v njem zajeti vsi bistveni elementi, ki so potrebni za izračun odboja svetlobe. V našem primeru bomo računali le odboj od sferičnih površin (krogel), ker pa je srce programa - račun zadetka krogle z žarkom - numerično zasnovan, odboj od poljubno ukrivljenih površin, ki se v sodobni optiki vse bolj uporabljajo, ne bi predstavljalo večjih težav.
Odboj svetlobe je v principu precej enostaven pojav: svetloba se od ravne površine odbije tako, da je odbojni kot (merjen od pravokotnice) enak vpadnemu (Slika 1):
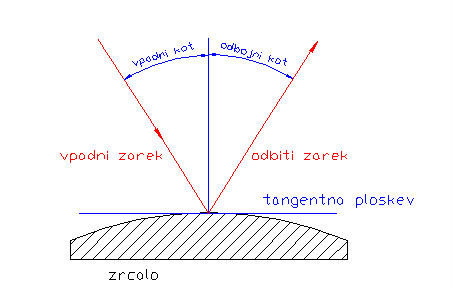
Slika1: Predstavitev odbojnega zakona
Pri ukrivljenih površinah, kakršne bomo mi obravnavali, pa moramo v točki, kjer svetloba pade na površino, poiskati TANGENTNO PLOSKEV. Nadalje obravnavamo odboj tako, kakor bi tangentna ploskev predstavljala ravno površino.
Mi bomo obravnavali odboj žarka od krogel. Da bi to lahko storili pa moramo najprej določiti, kje žarek zadane kroglo. Matematično gledano rešujemo problem preseka premice (ki predstavlja žarek) s kroglo (Slika 2):
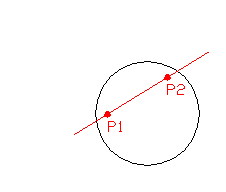
Slika2: Prikaz preseka krogle s premico.
Mi bomo enačbo premice zapisali v vektorski obliki, pri čemer bomo lego točke M na premici podali z začetno točko S(START) in smernim vektorjem D(DIRECTION), pomnoženim s parametrom t:
M=S+t*D
Premica zadane površino krogle tedaj, ko je oddaljenost točke na premici M od središča krogle C(CENTER) enaka polmeru krogle r:
Abs(M-C)=r
Enačbo kvadriramo, da se znebimo absolutne vrednosti. Vstavimo komponente vektorjev in dobimo:
![]()
Vstavimo enačbo premice:
![]()
Kvadriramo in uredimo:
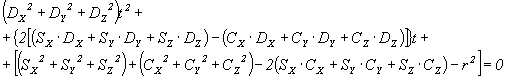
Dobili smo kvadratno enačbo za t:
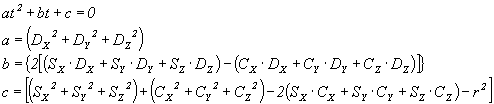
Rešimo enačbo in dobimo:
![]()
V splošnem ima enačba lahko:
a.) 2 realni rešitvi t1 in t2, če premica prebode kroglo (Slika 3a)
b.) eno dvojno realno rešitev t1=t2, če se premica krogle le dotakne (Slika 3b)
c.) 0 realnih rešitev, če premica zgreši kroglo (Slika 3c). Dobimo sicer kompleksne rešitve, ki pa za nas niso zanimive.
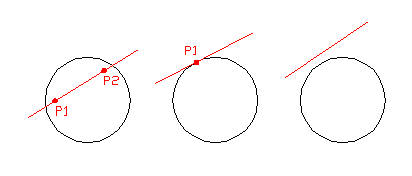
Slika3a Slika3b Slika3c
Za nas je zanimiv le primer a.), saj je edini, pri katerem pride do odboja. Ker se žarek od krogle odbije že v točki P1, je točka P2 nepomembna. Zanima nas torej lega točke P1(POINT). Izračunali jo bomo iz enačbe premice:
P1=S+t1*D
Pri reševanju si bomo pomagali z vektorsko algebro. Na Sliki3 je prikazana geometrija problema:
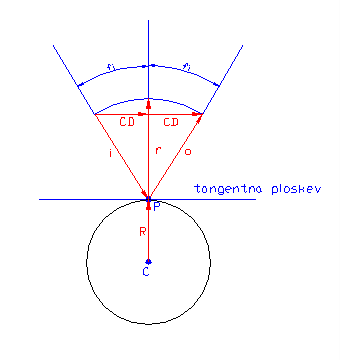
Slika3: Geometrija odboja žarka od krogle.
Vektor vpadnega žarka I(INCOMING) je enak smernemu vektorju premice D. Vektor normale na površino krogle v točki zadetka P je enak vektorju radija R=P-C. Iščemo vektor O(OUTGOING), ki nam bo povedal smer odbitega žarka. V izračunu bomo potrebovali enotske smerne vektorje (dolžine 1), ki jih bomo označili z malimi črkami (npr.I postane i itd.), zato bomo morali vektoja I in R normirati:
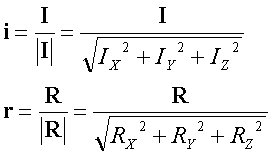
Po definiciji je skalarni produkt dveh vektorjev (A in B) enak produktu njunih absolutnih vrednosti in cosinusa vmesnega kota fi:
![]()
če sta vektorja enotska, je njuna absolutna vrednost enaka 1 in je njun skalarni produkt kar enak kosinusu vmesnega kota:
![]()
Lahko torej zapišemo:
i*r=cos(fi)
Vektor spremembe smeri CD(CHANGE of DIRECTION) je enak (Slika3):
CD=-i+r*cos(fi)
In končno vektor smeri odbitega žarka:
o=r*cos(fi)+CD
Sedaj imamo vse potrebne podatke, da lahko postopek ponovimo:
-točka zadetka P je naša nova začetna točka S.......S=P
-smer odbitega žarka i je naš nov smerni vektor D...D=i
Izračun torej ponovimo od točke 2.2. naprej.
Teoretične principe, ki smo jih navedli v 2. poglavju, lahko izkoristimo za izdelavo programa, ki bo izračunal odboj žarka med kroglami in nazadnje pot žarka tudi narisal. Tak program je ACOTRACE, ki je napisan v programskem jeziku FORTRAN. Izvorno kodo najdete v datoteki z imenom "acotrace.f90", ki je zapakirana znotraj datoteke acotrace.zip.
Za lažje razumevanje je program prepleten z opisi v angleščini, ki povedo, kaj posamezen del programa naredi. Opise ločujejo od ostalega dela programa KLICAJI. Na primer komentar
!Set the color of the spheres
pomeni, da se začenja del programa, ki bo določil barvo izrisa krogel.
Program ravno tako vsebuje opis spremenljivk. Na primer vrstica
!NOS=number-of-spheres
pove, da nam spremenljivka "NOS" pove celotno število krogel.
Poglejmo si podrobneje delovanje delovanje GLAVNEGA PROGRAMA. Program najprej pokliče knjižnico MSFLIB, ki je potrebna za grafične procedure:
!-------------------------MAIN PROGRAM------------------- USE MSFLIB
Nato deklarira spremenljivke:
implicit real*8 (b-h,j-z) !XYZ=direction of viewpoint !SPEED=speed of line drawing !SX=Scaling factor for the x,y,z coordinates integer(4) color !NOS=number-of-spheres !NOR=number-of-rays dimension SP(10,4),sr(10,3),dr(10,3),SNR(10),S(3),D(3),nr(10),C11(4) dimension sp0(10,4),sr0(10,4),dr0(10,4),view(3,2),DX(3),axes(3) !SP=data for 5 spheres !SR=rays start point !DR=direction of rays !SNR=Starting number-of-reflections for each sphere !C11=Circle1 data for drawing !NR=number-of-reflections per surface !scale=minimum and maximum coordinate of the coordinates of the viewport !DX=moving constant for the x,y,z coordinates !axes=sequence of axes character*12 filename character*1 axis1,axis2 !filename=name of the file to import !axis1,2=name of the axes TYPE (windowconfig) wc LOGICAL status /.FALSE./ !Defining the default values SNR=(/(9999.,i=1,10)/) speed=5000 !Set the background color bkcolor=SETBKCOLORRGB(#FFFFFF) !White CALL CLEARSCREEN($GCLEARSCREEN) !Set the color of the text color = SETTEXTCOLORRGB(#000000) !Black
Sledi izpis naslovne strani:
!-----------------------DATA INPUT----------------- !Welcome screen 100 CALL CLEARSCREEN($GCLEARSCREEN) write(*,*) write(*,*)' ACOTRACE' write(*,*) write(*,*)' A program for drawing the reflection of a beam of light' write(*,*)' between sheres, placed in space.' write(*,*) write(*,*)' by Gustin Bostjan' write(*,*) write(*,*)'-----------------------------------------------------------------------------'
Program ponudi dva načina vnosa podatkov: iz datoteke ali z ročnim vnašanjem:
write(*,*) write(*,*)'Do you want to input the data from a FILE or by TYPING?' write(*,*)'(1=FILE,2=TYPING)?' read(*,*)yn
Vnos iz datoteke:
!File Data import if (yn.eq.1) then write(*,*)'File name?' read(*,*)filename open(13,file=filename) read(13,*)speed read(13,*)nor read(13,*)((SR(i,j),j=1,3),i=1,nor) read(13,*)((DR(i,j),j=1,3),i=1,nor) read(13,*)nos read(13,*)((SP(i,j),j=1,4),i=1,nos) read(13,*)(SNR(i),i=1,nos) goto 140 endif
Ročno vnašanje podatkov:
!Typing data input 110 write(*,*)'How many spheres do you want (1-10)?' read(*,*)nos nos=int(nos) if(nos.gt.10) then write(*,*)'Number is not within range' goto 110 endif write(*,*)'Write the data for the spheres (x,y,z,r)' read(*,*)((sp(i,j),j=1,4),i=1,nos) 120 write(*,*)'How many rays do you want (1-10)?' read(*,*)nor nor=int(nor) if(nor.gt.10) then write(*,*)'Number is not within range' goto 120 endif write(*,*)'Write the data for the START POINTS of the RAYS (x,y,z)' read(*,*)((sr(i,j),j=1,3),i=1,nor) write(*,*)'Write the data for the DIRECTION VECTORS of the RAYS (x,y,z)' read(*,*)((dr(i,j),j=1,3),i=1,nor)
Sprememba nastavitev:
!Options input 140 write(*,*)'Do you want to change the OPTIONS (1=YES,2=NO)?' read(*,*)yn if (yn.ne.1) then goto 150 endif write(*,*)'Do you want to define the maximum Number-of-Reflections (NR) for each sphere' write(*,*)'(1=YES,2=NO)?' read(*,*)yn if (yn.eq.1) then write(*,*)'Write the maximum Number-of-Reflections (NR) for each sphere (NR1,NR2,..,NR10)' read(*,*)(SNR(i),i=1,nos) endif write(*,*)'Write the smoothig-of-drawing factor (ca.2000)' read(*,*)speed write(*,*)'Do you want to change the viewport' write(*,*)'(1=YES,2=NO)?' read(*,*)yn if (yn.ne.1) then goto 150 endif 130 write(*,*)'Which axis do you want to put the viewpoint above (X=1,Y=2,Z=3)' read(*,*)XYZ if (xyz.eq.1) then axis1='Z' axis2='Y' axes=(/3,1,2/) else if(xyz.eq.2) then axis1='X' axis2='Z' axes=(/1,2,3/) else if(xyz.eq.3) then axis1='Y' axis2='X' axes=(/2,3,1/) else write(*,*)'Number is not within range' goto 130 endif write(*,*)axis1,' points RIGHT, ',axis2,' points DOWN' write(*,*)'Write the MIN and MAX value of the ',axis1,'(horizontal) coord. of the viewport(min,max)' read(*,*)(view(1,i),i=1,2) write(*,*)'Write the MIN value of the ',axis2,'(vertical) coord. of the viewport' read(*,*)view(3,1) !-----------------------END OF DATA INPUT-----------------
Pretvorba dejanskih koordinat v koordinate zaslona
!Converting coordinates into screen coord. SX=800/(view(1,2)-view(1,1)) !view(axe(2),2)=view(axe(2),1)+800/SX do i=1,10 do j=1,4 sp0(i,j)=sp(i,j) sr0(i,j)=sr(i,j) dr0(i,j)=dr(i,j) enddo enddo DO I=1,3 DX(i)=-view(i,1) do j=1,10 sp(j,i)=int((sp0(j,axes(i))+dx(i))*SX) sr(j,i)=int((sr0(j,axes(i))+dx(i))*SX) dr(j,i)=dr0(j,axes(i)) enddo enddo do i=1,10 sp(i,4)=sp0(i,4)*SX enddo
Sledi nastavitev grafičnega načina 800x600:
!Start-up graphic routines !Set the graphics mode !Set the x & y pixels to 800X600 and font size to 8x12 150 wc.numxpixels = 800 wc.numypixels = 600 wc.numtextcols = -1 wc.numtextrows = -1 wc.numcolors = -1 wc.title= "ACOTRACE"C wc.fontsize = #0008000C if (.NOT.status) status = SETWINDOWCONFIG(wc)
Določanje barve ozadja in barve izrisa krogel:
!Fill with the background color bkcolor=FLOODFILLRGB(100,100,#FFFFFF) !Set the color of the spheres color = SETCOLORRGB(#000000) !Black
Izris krogel:
!Draw the spheres do i=1,nos do j=1,3 if(j.eq.1) then k=1. m=1. else if (j.eq.2) then k=.15 m=1. else if (j.eq.3) then k=1. m=.3 endif C11=(/sp(i,1)-k*SP(i,4),SP(i,3)-m*SP(i,4),SP(i,1)+k*SP(i,4),SP(i,3)+m*SP(i,4)/) !x1,y1,x2,y2 dummy = ELLIPSE($GBORDER,C11(1),C11(2),C11(3),C11(4)) enddo enddo
Določanje barve izrisa žarkov:
!Set the color of the rays color = SETCOLORRGB(#0000FF) !Red Določanje žarka, za katerega bo program izrisal odboj: !Defining current ray do n=1,nor D=(/(DR(n,i),i=1,3)/) S=(/(SR(n,i),i=1,3)/) NR=(/(SNR(i),i=1,10)/) CALL rekurz(S,D,NR,SP,speed) 200 enddo 300 end
Sledi razlaga REKURZIVNE SUBROUTINE "Rekurz":
!------------------------RECURSION START---------------------- recursive Subroutine rekurz(S,D,NR,SP,speed)
Vhodni podatki v "Rekurz" so začetna točka žarka(S), njegova smer(D), maksimalnon število odbojev od vsake krogle(NR), podatki o kroglah(SP) in hitrost izrisa žarkov(speed).
Delovanje rutine "Rekurz" bi lahko na kratko obnovili tako:
-sprejem vhodne podatke
-izračun in izris
-izdaja izhodnih podatkov, KI SO HKRATI VHODNI PODATKI ZA NASLEDNJI KORAK
Deklaracija spremenljivk:
USE MSFLIB implicit real*8 (b-h,j-z) !TT=parameter T for the nearest hit sphere !HIT=number of the sphere that was hit first !DI=discriminant of quadratic equation for ray and sphere intersection !K1,K2,K3=constants a,b,c of quadratic equation for ray and sphere iontersection implicit integer(2) (A) dimension S(3),D(3),C1(4),T(3),A(3),B(3),E(3) dimension EL(3),EC(3),CDV(3),NDV(3),SP(10,4),nR(10) !E=EndPoint of line !SP=data for 5 spheres !A=start point of line to draw !B=end point of line to draw !S=Start point of line !D=Direction of line !C1=Circle1 data !LL=line lenght !T=parameter for vector line notation !EL=unit vector in line direction !EC=unit vector in circle radius directio !cosfi=cosine of the angle between EL and EC !CDV=change-of-direction vector !NDV=new-direction vector !NR=number-of-reflections per surface TYPE (xycoord) xy !Setting the parameter KONEC, which says when to end program konec=0 !Norming the direction vector LL=sqrt(D(1)**2+D(2)**2+D(3)**2) D=(/(D(i)/LL,i=1,3)/)
Izračun presečišča žarka s kroglo:
!Intersection of line and sphere TT=1e9 do m=1,5 if (nr(m).lt.1)then goto 160 endif WW=0 c1=(/(sp(m,i),i=1,4)/) K1=0 K2=0 K3=0 do i=1,3 K1=K1+D(i)**2 K2=K2+2*S(i)*D(i)-2*D(i)*C1(i) K3=K3+S(i)**2+c1(i)**2-2*S(i)*C1(i) enddo K3=K3-c1(4)**2 DI=K2**2-4*K1*K3 if(DI.lt.0) then T(3)=1e8 goto 150 endif t1=(-K2+sqrt(DI))/2/K1 t2=(-K2-sqrt(DI))/2/K1 if (t2.gt.0) then t(3)=t2 else if (t1.gt.0) then t(3)=t1 else T(3)=1e8 goto 150 endif goto 150
Določitev najbližje izmed krogel, ki jih žarek seče:
!Defining the nearest hit sphere 150 if(T(3).lt.TT)then TT=T(3) HIT=m endif 160 enddo !Decrease the NR for the hit sphere by one NR(hit)=nr(hit)-1 !Generate data for the nearest hit sphere T(3)=TT E=(/(S(i)+T(3)*D(i),i=1,3)/) c1=(/(sp(hit,i),i=1,4)/) !Check if enpoint of line lies within view window (800x600) if ((E(1)>800).or.(E(1)<1).or.(E(3)<1).or.(E(3)>600)) then tt=1e7 endif
Izračun poti žarka v primeru, da ne zadane nobene krogle:
!If no sphere is hit, calculate ray path 170 if(tt.gt.1e6)then E=(/(S(i),i=1,3)/) t(3)=0 do while((e(1).le.800).and.(e(1).ge.0).and.(e(3).ge.0).and.(e(3).le.600)) t(3)=t(3)+1 E=(/(S(i)+T(3)*D(i),i=1,3)/) enddo konec=1 endif
Izris žarka:
!Draw line from the last hit sphere to destination A=(/(int(s(i)),i=1,3)/) CALL MOVETO(A(1),A(3),xy) do j=1,speed B=(/(int(s(i)+t(3)*j*d(i)/speed),i=1,3)/) status = LINETO(B(1),B(3)) enddo !End program if no spheres are hit to prevent it to !calculate new direction of line if (konec.eq.1) then goto 210 endif
Izračun nove smeri žarka po odboju od krogle:
!New direction of line when a sphere is hit EL=(/(-D(i),i=1,3)/) EC=(/((-C1(i)+E(i))/C1(4),i=1,3)/) cosfi=EL(1)*EC(1)+EL(2)*EC(2)+EL(3)*EC(3) do i=1,3 CDV(i)=-EL(i)+cosfi*EC(i) NDV(i)=cosfi*EC(i)+CDV(i) enddo S=(/(E(i)+.1*NDV(i),i=1,3)/) !x,y,z D=(/(NDV(i),i=1,3)/) !x,y,z
Klicanje novega koraka, pri čemer so izhodni podatki n-tega koraka vhodni podatki (n+1)-tega koraka:
call rekurz(S,D,NR,SP,speed) 210 return end !------------------------RECURSION END-------------------------
Rekurzija se ponavlja, dokler žarek ne zgreši vseh krogel. Ko se to zgodi, se vrne v "GLAVNI PROGRAM", kjer dobi podatke za novi žarek in postopek rekurzije se ponovi.
Program je shranjen pod imenom "acotrace.exe", najdete ga pa v datoteki acotrace.zip.
Program uporablja belo ozadje zaslona, da lahko izris enostavno prenesemo na Tiskalnik (sicer bi nam tiskalnik stiskal črno ozadje!). Zaslon posnamemo v Clipboard s tipko PRINTSCREEN in nato vnesemo v kakršenkoli program s CTRL+V.
Takoj po zagonu nas program vpraša, če želimo vnesti podatke iz datoteke ali s tipkanjem (Slika4):

Slika4: Naslovna stran programa.
Za lažje razumevanje je tekst opremljen s primerom: na koncu razlage vsakega koraka je v oklepaju zaporedje ukazov, ki jih za naš primer uporabimo. Ukazi so ločeni s podpičjem (;), gre pa v glavnem za pritisk na tipko ENTER in za vnašanje teksta, ki se nahaja med narekovaji ("text").
V položaju na Sliki4 vtipkamo "2" in potrdimo.... ("2";Enter).
Program nas vpraša, koliko krogel želimo vnesti. Vtipkamo število med 1 in 10........("2";Enter)
Naslednje vprašanje zadeva podatke o kroglah, ki zajemajo lego središča krogle (X, Y in Z koordinato) ter polmer krogle (R). V principu moramo vnesti le zaporedje števil (x1,y1,z1,r1,x2,y2,z2,r2,...), ki jih lahko ločimo z vejico ("10,20,...") ali z ENTER ("10";Enter;"20";Enter;...). Zaradi večje preglednosti podatke za vsako kroglo vnesemo v svojo vrstico.........("600,0,300,150";Enter;"200,0,300,100";Enter)
Program nas vpraša za število žarkov, ki naj bo med 1 in 10........("1";Enter)
Vnesemo lege izvorov posameznih žarkov (X, Y in Z koordinate).....("350,0,400";Enter)
Vnesemo smeri posameznih žarkov (X, Y in Z koordinate).......("100,0,-75";Enter)
Program nas vpraša, če želimo spremeniti nastavitve. Mi bomo nastavili PREDNASTAVLJENE VREDNOSTI in sicer zato, da uporabnik ve, kakšne sploh so prednastavljene vrednosti. Ker v bistvu ne bomo ničesar spremenili, lahko tu izberete ("2";Enter) in si sledeč tekst preberete kasneje, ko vas bodo zanimale nastavitve in prednastavljene vrednosti.
Izberemo torej ("1";Enter) in vnesimo PREDNASTAVLJENE VREDNOSTI.
Nastavimo največje dopustno število odbojev za vsako od desetih krogel posebaj. ("9999,9999,9999,9999,9999,9999,9999,9999,9999,9999";Enter)
Nastavimo faktor upočasnitve izrisa: 2x večje število povzroči 2x počasnejši izris in obratno. ("5000";Enter)
Izberemo spreminjanje pogleda....("1";Enter)
Izberemo os, iznad katere bomo opazovali dogajanje. Naša opazovalna lega bo v smeri izbrane osi in sicer neskončno oddaljeno (paralelna projekcija). če npr. izberemo os Y, bomo gledali pravokotno na ravnino XZ od "zgoraj" (od pozitivne smeri osi y)........("2";Enter)
Program nam pove, da bo na zaslonu X-os kazala DESNO, Z-os pa DOL. Vnesemo razpon X-koordinat, ki jih želimo opazovati...........("0,800";Enter)
Vnesemo še začetek razpona Z-koordinat. Maksimalna vrednost se bo izračunala tako, da bo merilo v obeh smereh enako............("0";Enter)
Sledi pavza, da si lahko ogledamo vnešene podatke (Slika5).

Slika5: Pogled na vnešene podatke
Za nadaljevanje pritisnemo katerokoli tipko in na zaslonu dobimo Sliko6:
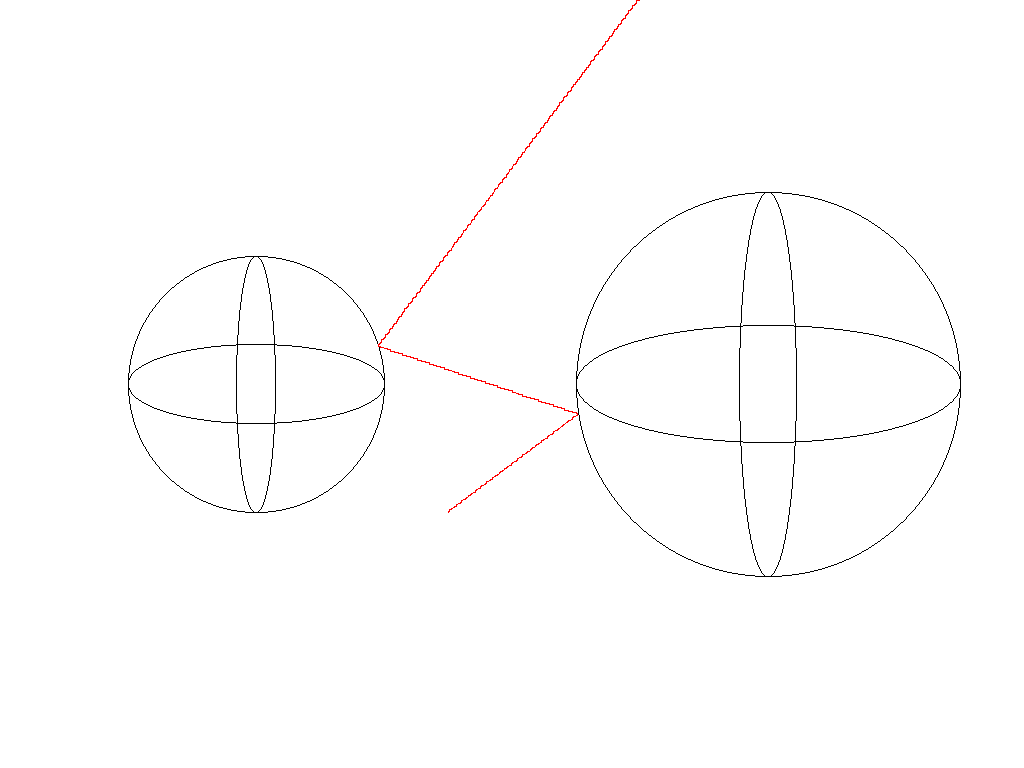
Slika6: Odboj žarka med dvema kroglama.....(dat1)
V datoteki "dat1", ki jo dobite z odpakiranjem acotrace.zip, se nahajajo enaki podatki, kot smo jih vnesli v poglavju 3.2.1.
V položaju na Sliki4 vtipkamo "1" in potrdimo........("1";Enter)
Program nas vpraša za ime datoteke. Vnesemo ime in potrdimo...........( "dat1";Enter)
Naslednje vprašanje zadeva nastavitve, ki so opisane v poglavju 3.2.1. Lahko bi jih spreminjali ("1";Enter), zaenkrat pa se zadovolimo s prednastavljenimi vrednostmi........("2";Enter)
Dobimo že znan izris, kakršen je prikazan na Sliki6.
Format zapisa bom razložil na primeru datoteke "dat1" z opisi, ki so ločeni s klicajem in se v datoteki ne nahajajo!
5000 !faktor upocasnitve izrisa
1 !število žarkov (=nor)
350 0 400 !startna tocka žarka (x,y,z)
100 0 -75 !smerni vektor žarka (x,y,z)
2 !število krogel (=nos)
600 0 300 150 !Podatki za 1. kroglo (x(1),y(1),z(1),r(1))
200 0 300 100 !Podatki za 2. kroglo (x(2),y(2),z(2),r(2))
21 22 !najvecje število odbojev od vsake krogle (snr(1),snr(2))
Primeri so shranjeni v datotekah oblike "dat*" znotraj komprimirane datoteke acotrace.zip in si jih lahko posnamete na računalnik, v program pa jih vnesete tako, kot je opisano v poglavju 3.2.2.
Na naslednjih straneh so predstavljeni izrisi, ki jih dobite iz posameznih primerov. Imena datotek so navedena v oklepajih po komentarju k sliki.
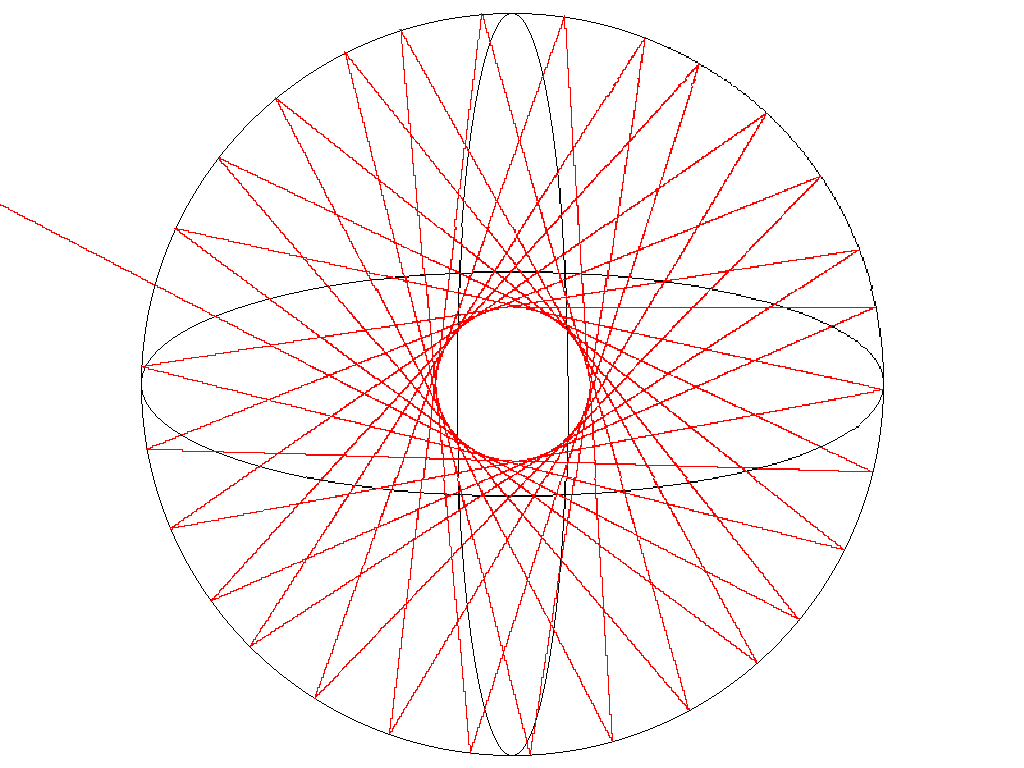
Slika7: Ravninski odboj žarka znotraj ene krogle.........(dat2)
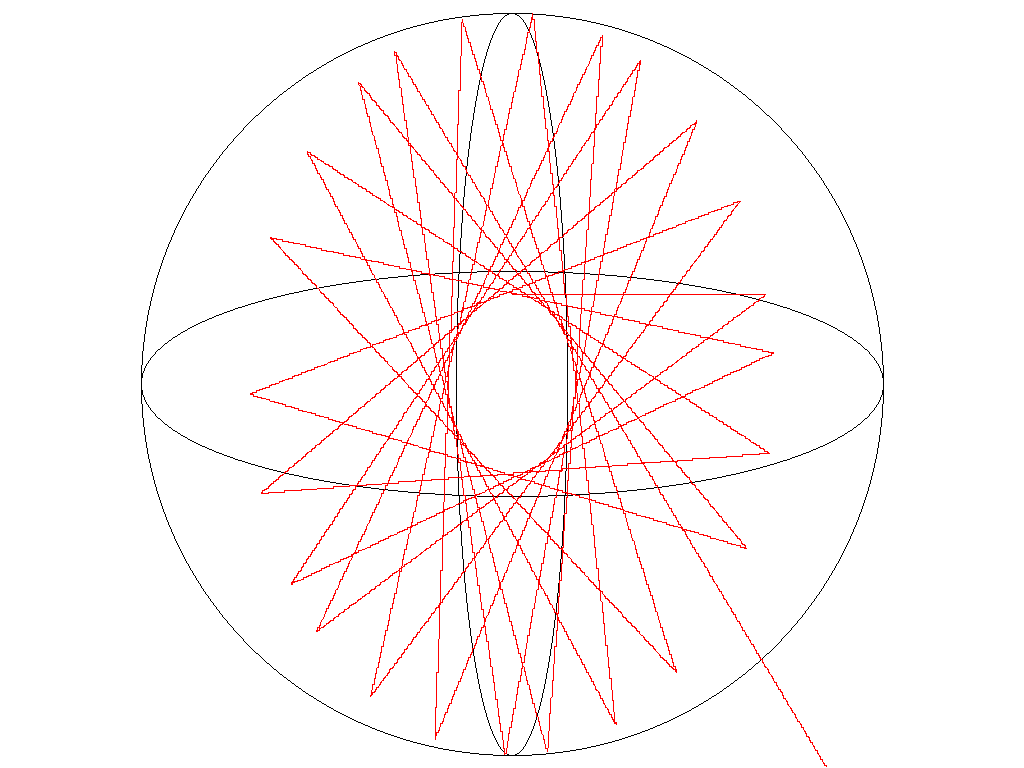
Slika8: Prostorski odboj žarka znotraj ene krogle.........(dat2)
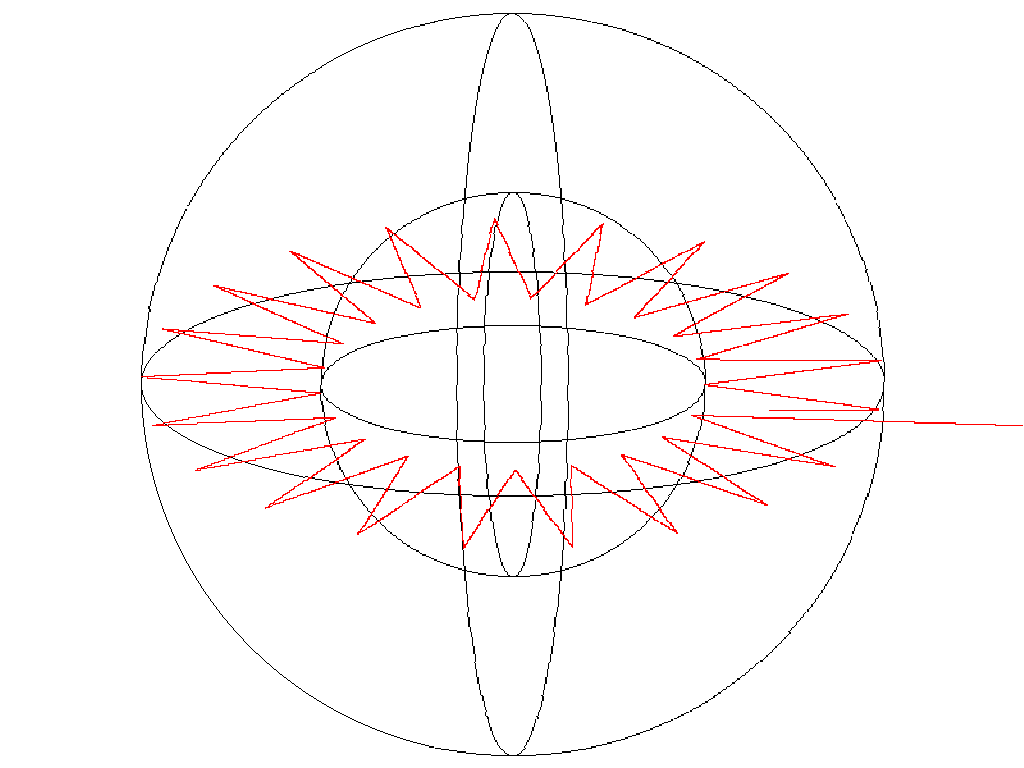
Slika9: Odboj žarka med dvema koncentričnima kroglama.........(dat5)
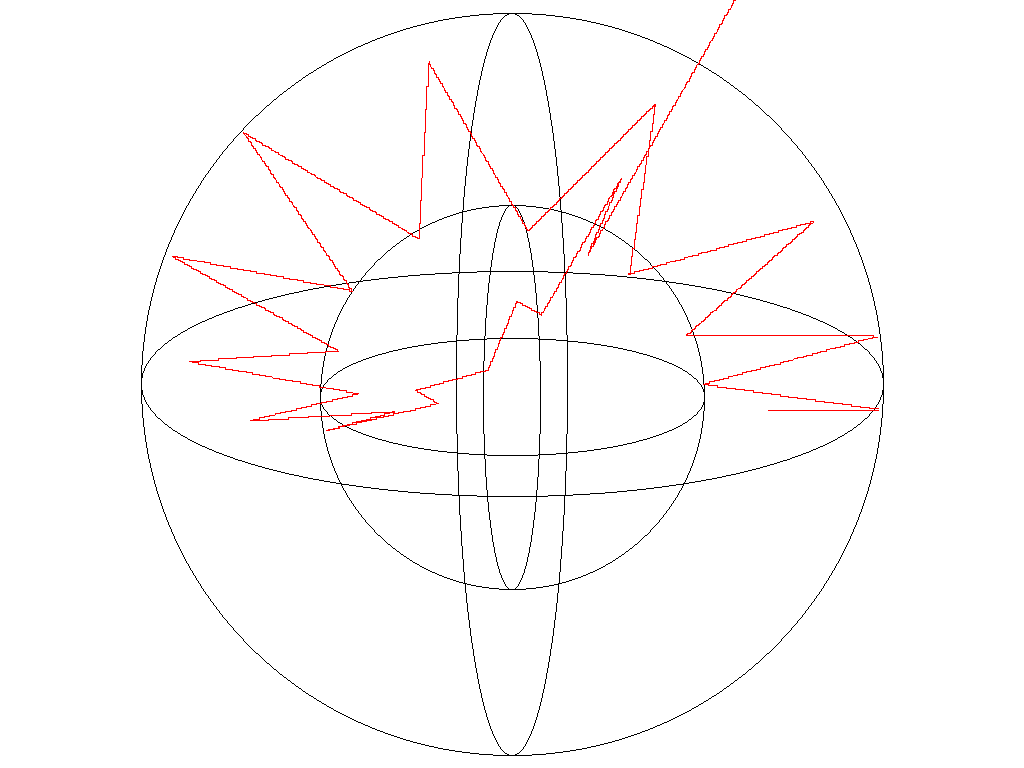
Slika10: Odboj žarka med dvema NE-koncentričnima kroglama.........(dat4)
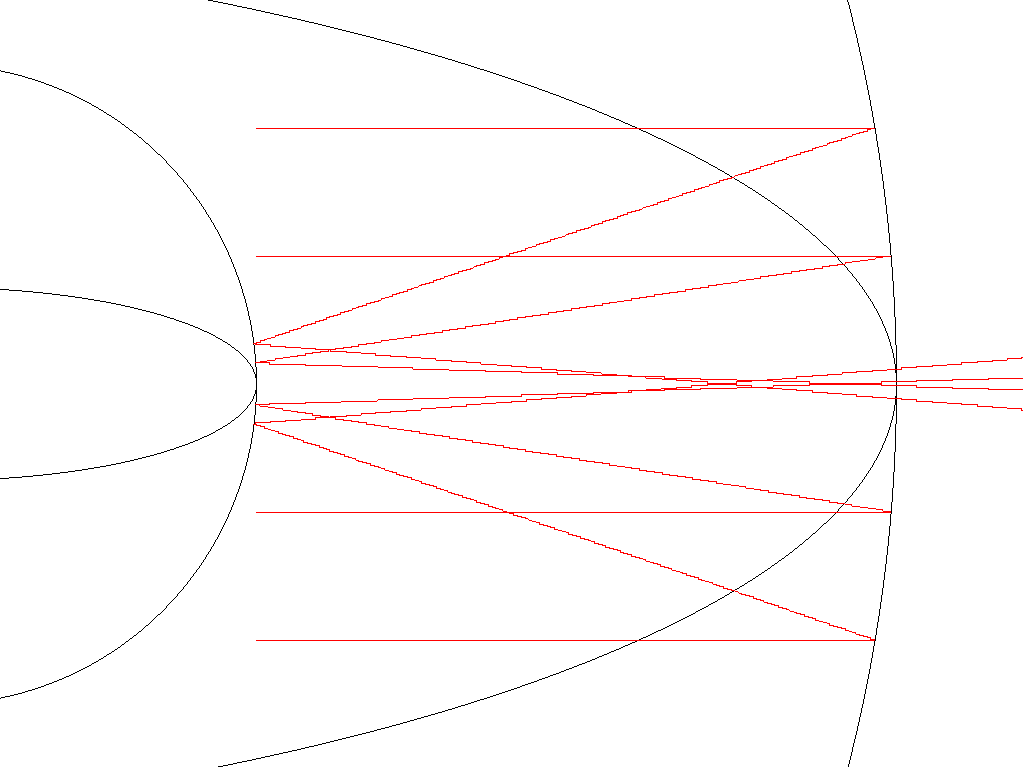
Slika11: Potek svetlobnih žarkov pri teleskopih tipa Cassegrain. Večja krogla predstavlja primarno zrcalo, manjša pa sekundarno zrcalo. Primerjaj s SlikoA v Uvodu..........(dat6)
Namen programa ACOTRACE je le predstavitev principa, preko katerega je možno izračunati odboj od sferične površine. Program bi lahko predelali za reševanje kompleksnejših nalog v optiki, vendar to presega meje tega seminarja, ki je bil namenjen zgolj ilustraciji osnovnih principov.
Kljub vsemu pa se iz primerov iz poglavja 3.3. lepo vidijo nekatere lastnosti odboja od krogel. Ena najzanimivejših je zame bila ta, da se žarek znotraj ene krogle vedno giblje v eni ravnini, ne glede na njegovo startno točko in smer (Slika7, Slika8) ter izriše zanimive, zvezdam podobne vzorce.
Enako velja za dve koncentrični krogli z različnima radiema (Slika9). šele pri NE-koncentričnih kroglah postane potovanje žarka prostorsko gibanje, ki bi ga težko sicer popisali.
Na Sliki11 je predstavljeno delovanje teleskopa tipa Cassegrain. Vidno je, da se žarki ne združijo v skupnem gorišču, zaradi česar slika ne bo ostra. Neosrtost je posledica sferične aberacije, ki jo odpravimo z uporabo asferičnih površin.