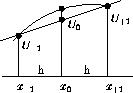
Ker smo pri numericnem izracunu najprej diskretizirali podrocje, smo dobili koncno stevilo tock, za katere mora veljati diferencialna enacba (1). Ker ne moremo zapisati tocnih odvodov v tocki se zadovoljimo s priblizki.

Splosno enacbo za funkcijo drugega reda, ki gre skozi tri aproksimacijske tocke zapisemo kot
Koeficiente a, b in c dolocimo tako, da gre funkcija 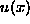 v tockah x = -h, x = 0 in x = -h zavzame vrednosti
v tockah x = -h, x = 0 in x = -h zavzame vrednosti 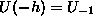 ,
,
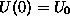 in
in 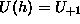 . Tako imamo tri enacbe iz katerih
izracunamo koeficiente
. Tako imamo tri enacbe iz katerih
izracunamo koeficiente
Ce zelimo izracunati odvod v tocko x = 0 odvajamo enacbo (7)
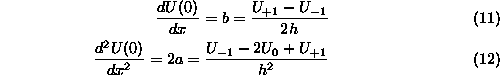
Enako pot uberemo pri integraciji enacbe (7)
kar je znano kot Simpson-ovo pravilo za numericno integracijo.